Page 123 - 인공지능 수학 교과서

곡선의 경사를 어떻게 수학적으로 표현할 수 있을까?

경사하강법 알고리즘의 핵심인 ‘경사’를 이해하는 데 필요한 수학적 개념으로 함수

의 극한과 미분에 대하여 살펴보자.

➊ 함수의 극한

함수 f(x)에 대하여 x의 값이 a가 아니면서 a에 한없이 가까워질 때, f(x)의 값이

일정한 값 L에 한없이 가까워지면 함수 f(x)는 L에 수렴한다고 한다. 이때 L을 x=a
에서 함수 f(x)의 극한값 또는 극한이라 하고, 기호로 다음과 같이 나타낸다.

▶ 기호 lim는 limit(극한)
x ~ a일 때, f(x) ~ L 또는 ^x~a f(x)=L
의 약자이다.

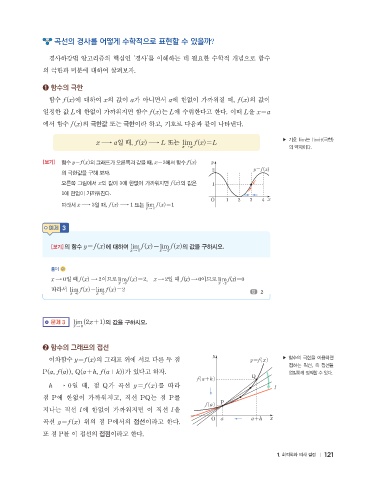
[보기] 함수 y=f(x)의 그래프가 오른쪽과 같을 때, x=3에서 함수 f(x) y
2 y=f(x)
의 극한값을 구해 보자.
오른쪽 그림에서 x의 값이 3에 한없이 가까워지면 f(x)의 값은 1

1에 한없이 가까워진다.
O 1 2 3 4 x
따라서 x ~ 3일 때, f(x) ~ 1 또는 ^x~3 f(x)=1

예제 3

[보기] 의 함수 y=f(x)에 대하여 ^x~0 f(x)- ^x~2 f(x)의 값을 구하시오.

풀이
x r 0일 때 f(x) r 2이므로 ^x=0 f(x)=2, x r 2일 때 f(x) r 0이므로 ^x=2 f(x)=0
따라서 ^x=0 f(x)- ^x=2 f(x)=2
답 2

문제 3 ^x~0 (2x+1)의 값을 구하시오.

➋ 함수의 그래프의 접선
y y
이차함수 y=f(x)의 그래프 위에 서로 다른 두 점 y=f(x) ▶ 함수의 극한을 이용하면 y=f(x)=(x-2)Û`+1
접하는 직선, 즉 접선을
5
P(a, f(a)), Q(a+h, f(a+h))가 있다고 하자. Q 엄밀하게 정의할 수 있다.
f(a+h)
h ~ 0일 때, 점 Q가 곡선 y=f (x)를 따라 l

점 P에 한없이 가까워지고, 직선 PQ는 점 P를 2
f(a) P 1
지나는 직선 l 에 한없이 가까워지면 이 직선 l 을
O a a+h x O 1 2 3 4 x
곡선 y=f(x) 위의 점 P에서의 접선이라고 한다.
또 점 P를 이 접선의 접점이라고 한다.

1. 최적화와 의사 결정 121